[백준] 구간 합 구하기(2042번)

문제 링크

 

풀이

쉬운 문제는 아닙니다. 세그먼트 트리를 이용해야 합니다. 먼저 배열을 통해 살펴보겠습니다.

 

1. 구간 합 구하기

2. 특정 위치 값 변경

 

1번의 경우 점화식을 이용해서 푼다면 다음과 같으므로 O(N)입니다. 

s[0] = a[0];
for (int i = 1; i < n; ++i)
{
	s[1] = s[i-1] + a[i];
}

 

2번은 a[4] = 3;의 방법으로 이루어지기 때문에 O(1)입니다. 1번이 M번, 2번이 K번 이루어진다면 O(NM + K)입니다. 문제에서 N, M, K는 적은 숫자가 아니기 때문에 O(NM + K)는 충분히 오래 걸릴 수 있습니다. 세그먼트 트리를 이용하면 O((M+K)*log₂N)에 가능합니다. O(NM + K)와 크게 다르지 않은 것처럼 보일 수 있는데, 문제에서 주어진 것처럼 N의 최대가 1,000,000이라면 log₂(1,000,000)는 약 20입니다. 시간복잡도를 계산할 때 로그의 밑은 의미가 없다고 하는데, 여기에선 정확한 계산을 위해 표기했습니다.

 

세그먼트 트리를 구성할 때 이진 탐색을 이용하기 때문에 리프 노드에는 배열의 수가 차례대로 들어갑니다. 그 외의 노드는 자식 노드의 합을 저장할 것이므로 루트 노드는 주어진 수를 모두 더한 값을 갖고 있게 됩니다. 아래 트리에서 리프 노드는 배열의 인덱스입니다. 리프 노드에 배열의 값이 그대로 들어가는 원리를 설명하는 부분은 아래에 등장합니다. 범위로 되어 있는 노드는 해당 범위의 구간 합입니다. 

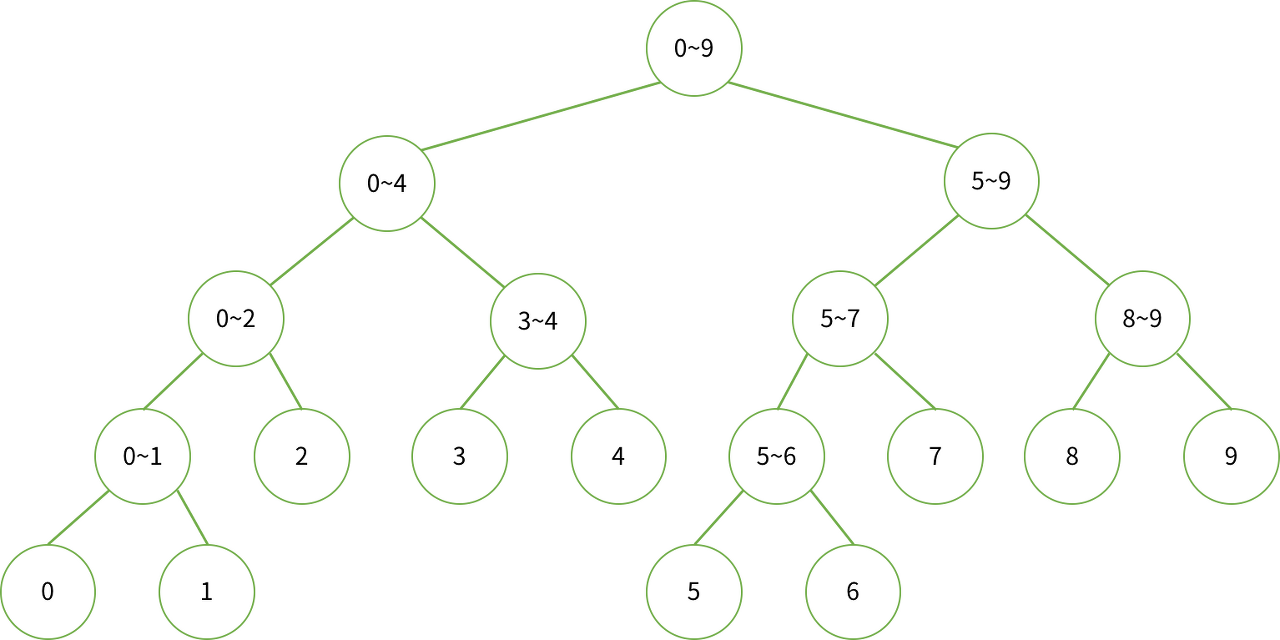
출처:BOJ

세그먼트 트리 만들기

노드의 개수를 먼저 정해야 합니다. N의 개수가 2의 승수일 때 완전 이진 트리가 되므로 노드의 개수가 딱 맞아떨어집니다. 주어진 데이터가 N개 일 때 2^(⌈log₂N⌉ + 1) - 1입니다. ⌈⌉는 천장 함수를 나타내는 표기로서 올림 함수라고도 합니다. N이 2의 승수라면 노드의 개수는 2*N - 1이기도 합니다. 위의 수식을 풀어쓴 것뿐입니다. N이 2의 승수이면 log₂N은 정수가 나오지만 그렇지 않을 경우엔 실수이므로 올려야 합니다. 노드의 개수가 모자라면 안 되니까요. 코드로 나타내면 다음과 같습니다.

	int h = ceil(log2(n));
	int tree_size = (1 << (h + 1));

코드에서는 -1 연산을 하지 않았습니다. 왜냐하면 노드를 0번이 아니라 1번 노드부터 시작할 것입니다. 그렇게 하면 자식 노드의 번호를 구하기 쉬운데 1번 노드의 왼쪽 자식 노드 번호는 2*1이이며 오른쪽 자식 노드 번호는 2*1 + 1가 됩니다. 3번 노드의 왼쪽 자식 노드 번호는 3*2, 오른쪽 자식 노드의 번호는 3*2 + 1입니다. 왜냐하면 노드에 번호를 붙일 때 다음과 같기 때문입니다.

리프 노드에 배열 값이 차례대로 들어갈 수 있는 이유를 0~1 노드를 통해 설명하겠습니다. 기본적으로 재귀함수로 구현하는 트리는 이진 탐색을 진행하게 되는데, 아래 노드에 접근할 때 중간값을 구해서(mid) 왼쪽 자식 노드는 start ~ mid, 오른쪽 자식 노드는 mid + 1, end 구간을 정해줍니다. 부모 노드가 0~1일 경우 왼쪽 자식 노드는 0~0이 되며 오른쪽 자식 노드는 1~1이 됩니다. 즉 start == end 조건이 만족하는 노드가 리프 노드가 되어, 해당 노드에 array[start] 값을 배정해주는 식으로 초기화를 진행할 겁니다. 그리고 리프 노드가 아닌 노드는 자식 노드의 합으로 초기화해줍니다. 이 과정을 반복하면 리프 노드가 아닌 노드들은 기본적으로 구간 합을 갖게 됩니다. 초기화 부분을 코드로 나타내면 다음과 같습니다.

long long init(vector<long long>& tree, vector<long long>& arr, int node, int start, int end)
{
	if (start == end) 
		return tree[node] = arr[end];
	else 
	{
		int mid = (start + end) / 2;		
		return tree[node] = init(tree, arr, node * 2, start, mid) + 
			            init(tree, arr, node * 2 + 1, mid + 1, end);
	}
}

 

구간 합

다음과 같이 표현할 수 있습니다. 다음은 5~8의 구간 합을 나타냅니다.

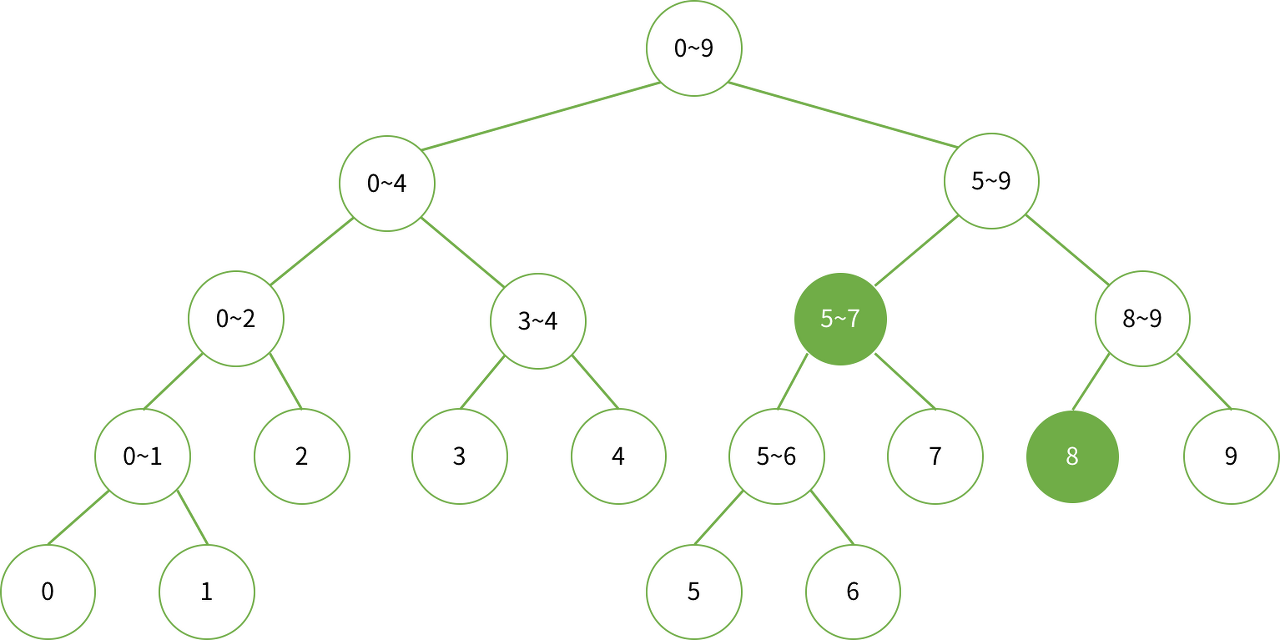
출처:BOJ

1번 노드를 시작으로 우리가 찾으려고 하는 배열의 인덱스 범위를 찾아가는 연산을 해야 합니다. 구간 합의 시작 구간을 [sum_start, sum_end]라고 하고 각 노드가 가지고 있는 구간을 [start, end]라고 하겠습니다. 참고로 구간을 나타내는 표기는 [a, b]와 (a, b)가 있는데요. [a, b]는 닫힌 구간(폐구간)이라고 하며 a와 b를 포함하는 구간입니다(a ≤ x ≤ b). (a, b)는 열린구간(개구간)이라고 하며 a, b를 미포함합니다(a < x < b). 리프 노드는 start == end인 상태를 말하며 아래에 나올 코드에서 이유를 확인할 수 있습니다. [sum_start, sum_end]와 [start, end]는 다음의 네 가지 경우의 수가 나옵니다.

 

1. 전혀 겹치지 않는 경우 -> 더 이상 탐색할 필요가 없습니다

2. [sum_start, sum_end] 안에 [start, end]가 완전히 포함되어 있는 경우 -> 현재 노드를 반환합니다

3. [start, end]안에 [sum_start, sum_end]가 완전히 포함되어 있는 경우 -> 자식 노드로 탐색을 더 진행합니다

4. 부분적으로 겹쳐 있는 경우 -> 자식 노드로 탐색을 더 진행합니다

 

1번의 경우 현재 노드에서 겹치는 부분이 없다면 더 이상 자식 노드를 탐색하는 의미가 없기 때문에 탐색을 이어나가는 의미가 없습니다. 구간 합을 구하는 부분이므로 0을 반환하면 됩니다.

 

2번의 경우 탐색을 진행하지 않고 현재 노드를 반환하면 되는데, 탐색을 진행할수록 구간이 작아지기 때문에 더 내려갈 필요가 없습니다.

 

3번이 2번과 조금 헷갈릴 수 있습니다. 3번의 경우 현재의 노드가 갖고 있는 구간이 구간 합보다 크기 때문에, 노드의 구간을 좁히기 위해 탐색을 더 진행해야 합니다.

 

4번은 3번과 비슷합니다.  구간 합에 필요한 노드의 구간을 정확하게 찾기 위해서 탐색을 더 진행해야 합니다.

 

코드로 표현하면 다음과 같습니다.

long long sum(vector<long long>& tree, int node, int start, int end, int sum_start, int sum_end)
{
	if (start > sum_end  || sum_start > end) return 0;
	else if (sum_start <= start && end <= sum_end ) return tree[node];
	else
	{
		int mid = (start + end) / 2;
		return sum(tree, node * 2, start, mid, sum_start, sum_end) + 
		       sum(tree, node * 2 + 1, mid + 1, end, sum_start, sum_end);
	}
}

1번처럼 겹치는 구간이 없다는 것은 [sum_start, sum_end]가 start보다 작은 범위에 있거나 end보다 큰 범위에 있는 경우를 말합니다.

 

특정 값 변경하기

init 함수와 별로 다르지 않습니다. 두 가지 방법을 쓸 수 있는데, init 함수를 통해 변경된 값으로 트리를 재구성하거나, update 함수를 만들어 변경 전의 값과 변경될 값의 변화량을 이용해 변경될 노드만 접근하는 것입니다. 백준에서 구간 합 구하기 문제에서는 init 함수로 트리를 재구성하는 방법을 사용하면 시간 초과가 발생합니다. 그래서 update 함수를 만들어서 값 변경에 영향을 받는 노드만 연산을 진행하겠습니다. init 함수를 이해했으면 update 함수는 쉽습니다.

void update(vector<long long>& tree, int node, int start, int end, int index, long long diff)
{
	if (index < start || index > end) return;
	tree[node] = tree[node] + diff;
	if (end != start)
	{
		int mid = (start + end) / 2;
		update(tree, node * 2, start, mid, index, diff);
		update(tree, node * 2 + 1, mid + 1, end, index, diff);
	}
}

 

코드

#include <vector>
#include <cstdio>
#include <cmath>
using namespace std;

long long init(vector<long long>& tree, vector<long long>& arr, int node, int start, int end)
{
	if (start == end) 
		return tree[node] = arr[end];
	else 
	{
		int mid = (start + end) / 2;		
		return tree[node] = init(tree, arr, node * 2, start, mid) + 
                                    init(tree, arr, node * 2 + 1, mid + 1, end);
	}
}

long long sum(vector<long long>& tree, int node, int start, int end, int sum_start, int sum_end)
{
	if (start > sum_end  || sum_start > end) return 0;
	else if (sum_start <= start && end <= sum_end ) return tree[node];
	else
	{
		int mid = (start + end) / 2;
		return sum(tree, node * 2, start, mid, sum_start, sum_end) + 
                       sum(tree, node * 2 + 1, mid + 1, end, sum_start, sum_end);
	}
}

void update(vector<long long>& tree, int node, int start, int end, int index, long long diff)
{
	if (index < start || index > end) return;
	tree[node] = tree[node] + diff;
	if (end != start)
	{
		int mid = (start + end) / 2;
		update(tree, node * 2, start, mid, index, diff);
		update(tree, node * 2 + 1, mid + 1, end, index, diff);
	}
}

int main()
{
	int n, m, k;
	scanf("%d %d %d", &n, &m, &k);
	m += k;
	vector<long long> arr(n);
	int h = ceil(log2(n));
	int tree_size = (1 << (h + 1));
	vector<long long> tree(tree_size);

	for (int i = 0; i < n; ++i)
		scanf("%lld", &arr[i]);
	
	init(tree, arr, 1, 0, n - 1);
	while (m--)
	{
		int a;
		scanf("%d", &a);
		if (1 == a) // b번째 수를 c로 변경
		{
			int b;
			long long c;
			scanf("%d %lld", &b, &c);
			b -= 1;
			long long diff = c - arr[b];
			arr[b] = c;
			update(tree, 1, 0, n - 1, b, diff);
		}
		else if (2 == a) // 구간 합 (b~c)
		{
			int b, c;
			scanf("%d %d", &b, &c);
			printf("%lld\n", sum(tree, 1, 0, n - 1, b - 1, c - 1));
		}
	}
}